# Puzzle 238 from the New Scientist

Solution

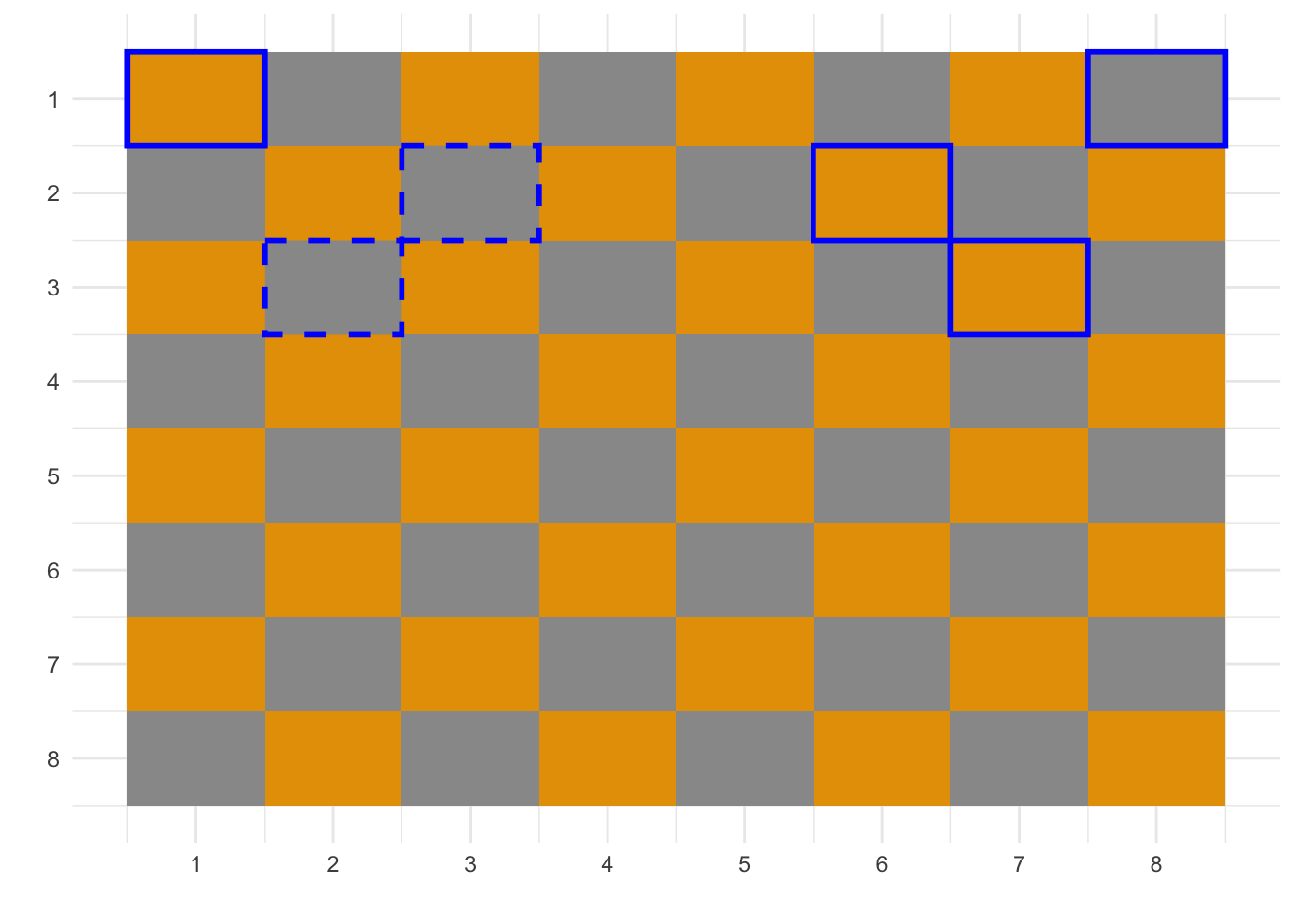
We start from a black square at the top left-hand quarter (highlighted area). There are only 8 black squares we can choose from (I use grey, instead of black).

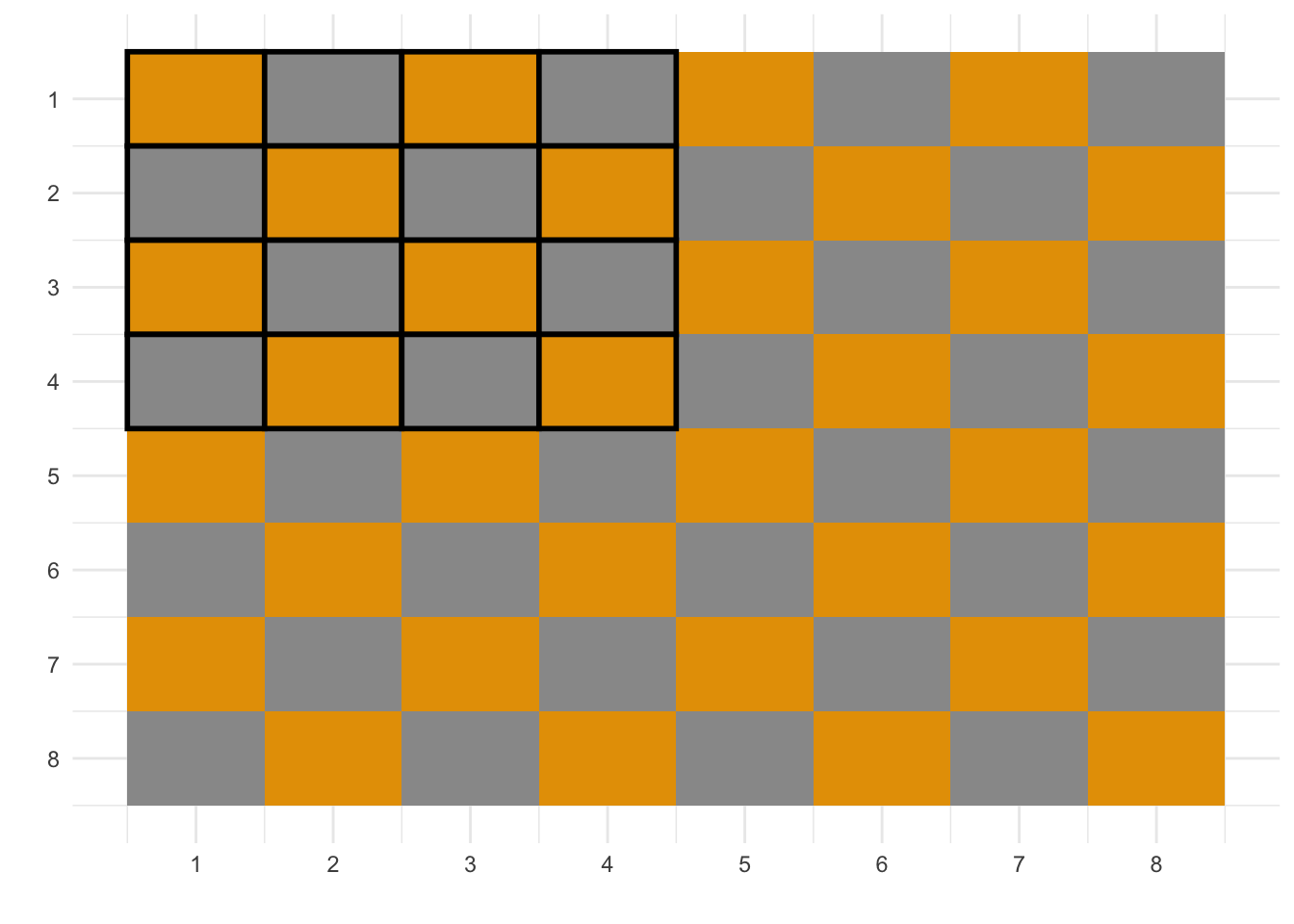
Since after 3 hops, there were now no squares she could move to that she hadn’t already visited the ending square needs to be at the edge of the board. This gives us 3 options as ending squares and 4 as starting ones. Out of which only {2, 3} and {3, 2} satisfy our requirements (highlighted below). From the other 2 ({3, 4} and {4, 3}) it’s impossible to arrive at the edge of the board after 3 steps and move to a square she hadn’t visited before.

My notation {2, 3} corresponds to {x, y} axes, respectively.

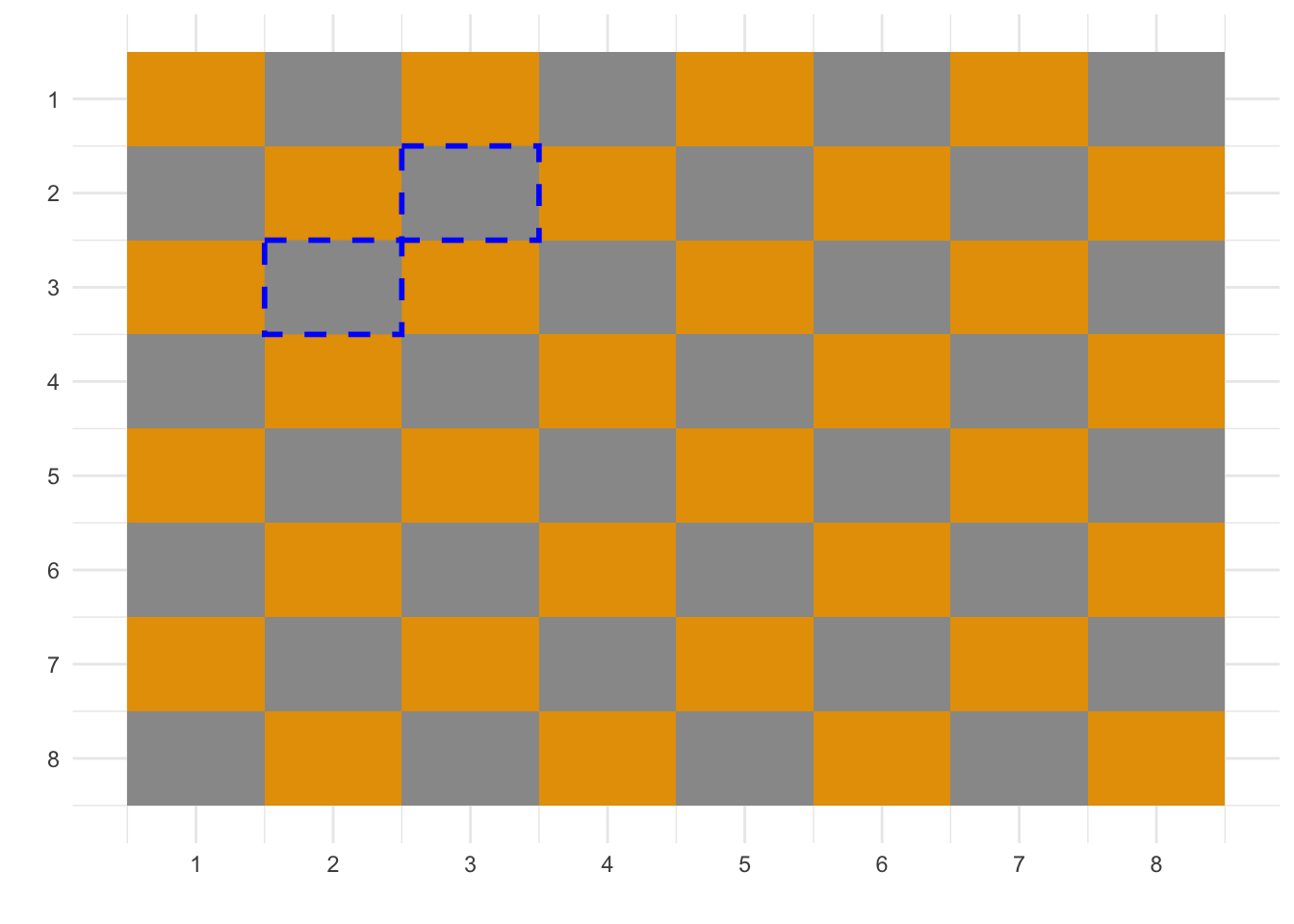
The starting square is {2, 3} or {3, 2}.

Further, we already know the final square (after the 3 hops). It is {1, 1}. The 2 remaining squares (these are {1, 3} and {3, 1}) have 3 or more squares the knight can jump to which makes it impossible to have covered them during the first 3 steps.

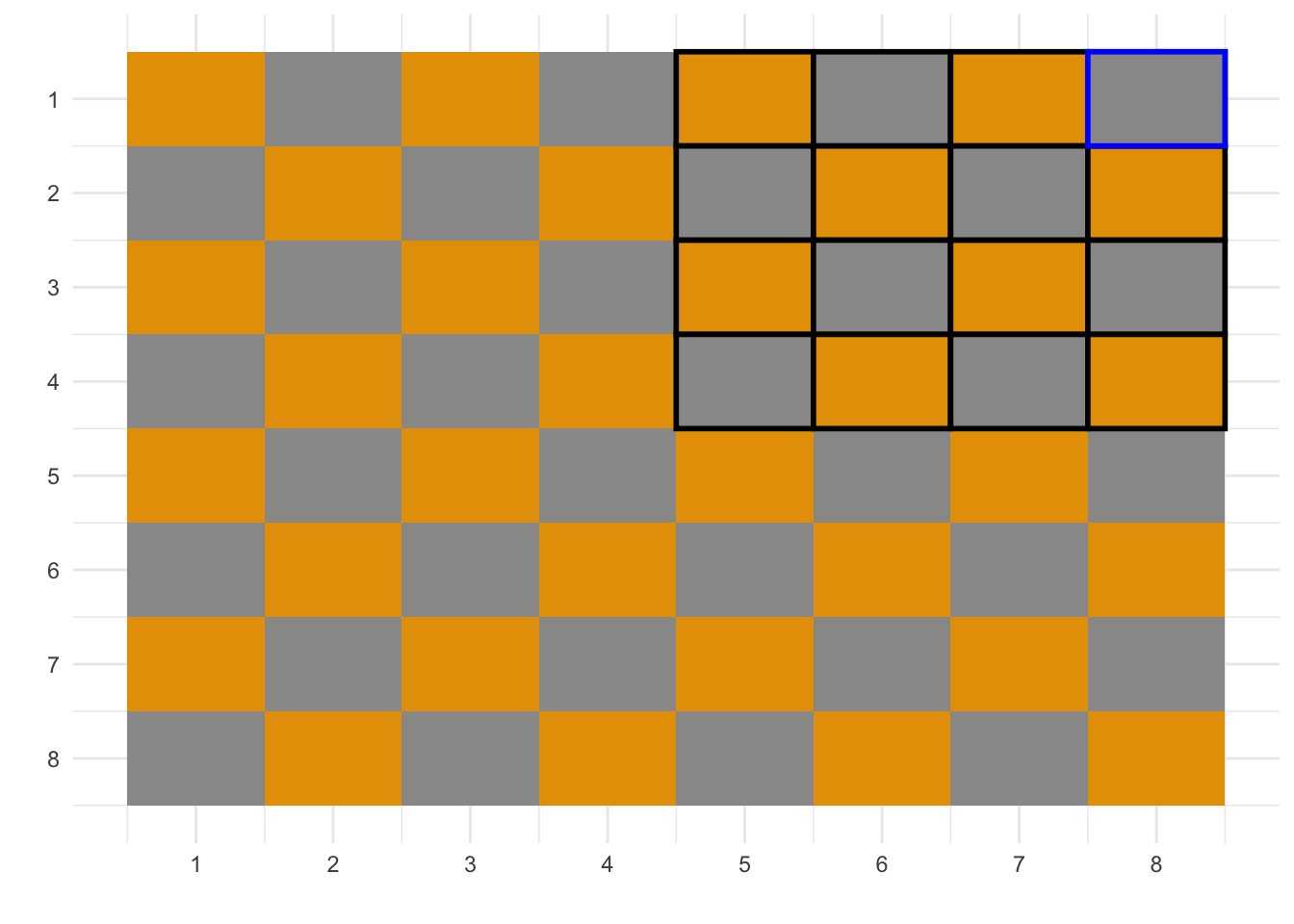
Then, we know we need to visit “at least one square in every column.” This means we need to end on the right-had side of the board. Further, we need to make “exactly one hop into the lower half of the board.” This means we will be ending up on the top right-hand quarter (highlighted area).

We further know the ending square, which is {8, 1} (highlighted). This is because there need to be no squares we can move that we hadn’t visited before. The same reasoning as before applies. The chessboard is symmetric after all!

We also know we need to pass from {6, 2} and {7, 3} since only from those 2 we can arrive at {8, 1} and have no square we haven’t moved before.

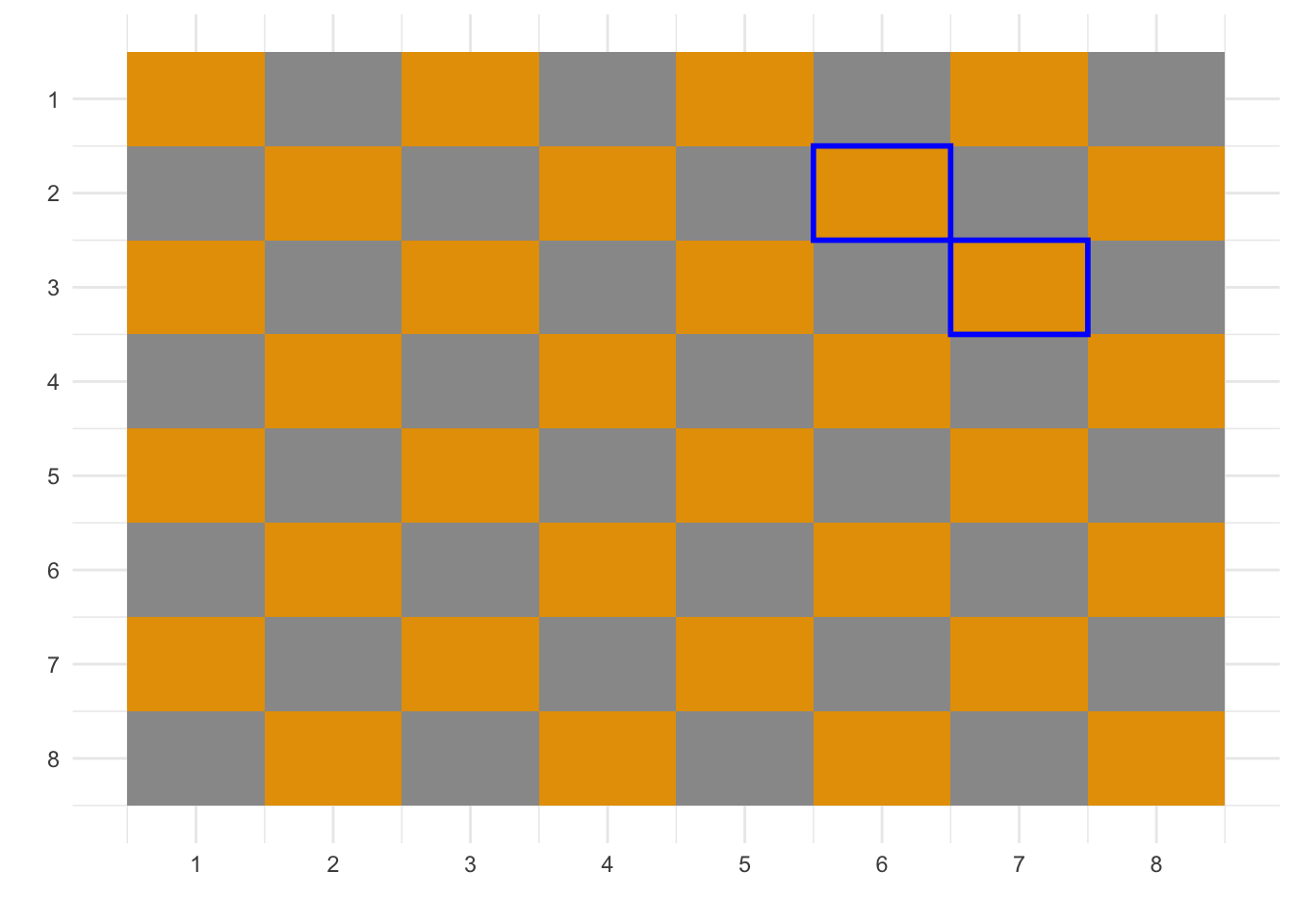
The ending square is {8, 1} and we need to pass from {6, 2} and {7, 3}.

So far, we know we start at either {2, 3} or {3, 2}, we make 3 moves ending in {1, 1}, we retrace our steps, and then make another 6 moves that bring us to {8, 1}, passing through {6, 2} and {7, 3}. We now need to find the intermediate moves.

To find the solution I coded the moves of a knight based on the specifications of the problem (knight_moves() and final_path()). The code needs as input a starting position and the number of moves.

# Function to simulate knight moves
knight_moves <- function(start_pos, num_moves) {
   # start_pos: the starting position
   # num_moves: the number of moves 
   
   # possible moves for the knight
   moves <- matrix(c(2, 1, -2, -1, 2, -1, -2, 1, 1, 2, -1, -2, 1, -2, -1, 2),
                   ncol = 2, byrow = TRUE)
   
   # function to check if the position is valid on an 8x8 chessboard
   is_valid_pos <- function(coord) {
      x <- coord[1]
      y <- coord[2]
      return(x >= 1 && x <= 8 && y >= 1 && y <= 8)
    }
    
    # starting position
    path <- list(start_pos)
    
    # simulating knight moves
    for (i in 1:num_moves) {
        curr_pos <- path[[i]]
        
        # generating all possible next moves
        next_moves_x <- curr_pos[1] + moves[,1]
        next_moves_y <- curr_pos[2] + moves[,2]
        
        next_moves <- matrix(c(next_moves_x, next_moves_y),
                             ncol = 2, byrow = F)
        
        # filtering valid moves
        next_moves <- next_moves[apply(next_moves, 1, is_valid_pos), ]
        
        # randomly selecting the next move
        next_move <- next_moves[sample(nrow(next_moves), 1), ]
        path <- append(path, list(next_move))
    }
    
    return(path)
}

# Function to implement the additional restrictions
final_path <- function(start_pos, num_moves){
   # start_pos: the starting position
   # num_moves: the number of moves 
   
   # simulate a knight's path 
   any_path <- knight_moves(start_pos, num_moves)
    
   path_matrix <- matrix(unlist(any_path), ncol = 2, byrow = T)
    
    ### add additional restrictions 
    
    # visit at least one square in every column 
    every_col <- seq(1, 8, by = 1)
    res1 <- every_col %in% path_matrix[, 1]
    
    # make exactly one hop into the lower half of the board
    lower_half <- 4
    res2 <- path_matrix[, 2] > lower_half

    # last square must be {8,1}
    res3 <- path_matrix[10, ] == c(8, 1)
    
    # need to be at {2, 3} (or {3, 2}) after 1st move and {3, 2} (or {2, 3}) at 3rd move
    res4 <- (path_matrix[2, ] == c(3, 2) & path_matrix[4, ] == c(2, 3)) |
       (path_matrix[4, ] == c(3, 2) & path_matrix[2, ] == c(2, 3))
    
    # need to be at {6, 2} (or {7, 3}) at 7th move and {7, 3} (or {6, 2}) at 8th move
    res5 <- (path_matrix[9, ] == c(6, 2) & path_matrix[7, ] == c(7, 3)) |
       (path_matrix[7, ] == c(6, 2) & path_matrix[9, ] == c(7, 3))
    
    
    while(sum(res1) != 8 | sum(res2) != 1 | sum(res3) != 2 | sum(res4) != 2 | sum(res5) != 2) {
     
        any_path <- knight_moves(start_pos, num_moves)
        
        path_matrix <- matrix(unlist(any_path), ncol = 2, byrow = T)
        
        # visit at least one square in every column 
        res1 <- every_col %in% path_matrix[, 1]
        
        # make exactly one hop into the lower half of the board
        res2 <- path_matrix[, 2] > lower_half
       
        # last square must be {8,1}
        res3 <- path_matrix[10, ] == c(8, 1)
        
        # need to be at {2, 3} (or {3, 2}) after 1st move and {3, 2} (or {2, 3}) at 3rd move
        res4 <- (path_matrix[2, ] == c(3, 2) & path_matrix[4, ] == c(2, 3)) |
           (path_matrix[4, ] == c(3, 2) & path_matrix[2, ] == c(2, 3))
        
        # need to be at {6, 2} (or {7, 3}) at 7th move and {7, 3} (or {6, 2}) at 8th move
        res5 <- (path_matrix[9, ] == c(6, 2) & path_matrix[7, ] == c(7, 3)) |
           (path_matrix[7, ] == c(6, 2) & path_matrix[9, ] == c(7, 3))
        
    }
    
    return(any_path)
    
}

For example, starting {1, 1} and after 9 moves we cover the following path:

# it runs for a few seconds/minutes until it finds a solution
set.seed(3)
res <- final_path(start_pos = c(1, 1), num_moves = 9)

## Move # 1 :  1 1 
## Move # 2 :  2 3 
## Move # 3 :  4 4 
## Move # 4 :  3 2 
## Move # 5 :  5 3 
## Move # 6 :  6 5 
## Move # 7 :  7 3 
## Move # 8 :  8 1 
## Move # 9 :  6 2 
## Move # 10 :  8 1

Of course, the results will be different each time the code is run. So I re-run the code 20 times and keep only the distinct solutions. We end up with 5 distinct solutions. The figure shows the sequence of moves (labels 1-10) and the visited squares (in purple) for each of the 5 solutions.

Note, for some solutions we visit the same square twice. For example, in the 2nd solution the square {4, 4} is visited in moves 3 and 5.

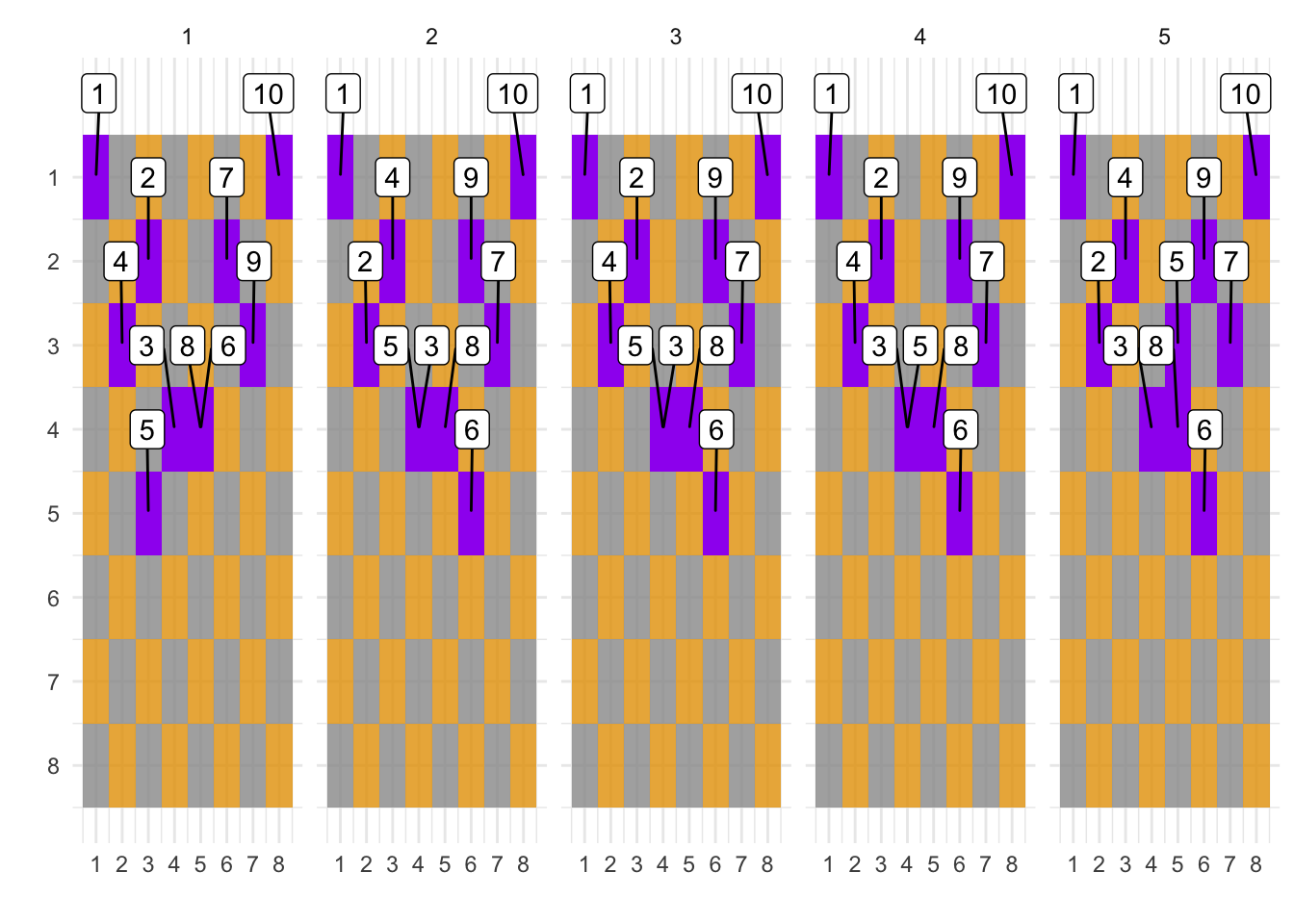
So my answer to the puzzle is apparently: “No”, we can’t retrace the knight’s path. She could have taken any of the 5 paths.

The published solution corresponds to solution 5 above. It is the only one where the knight doesn’t visit the same square more than once. I’m guessing this is a prerequisite (?), that’s why they disregard all the others.